La cuestión más importante que aún no se ha respondido sobre el número Pi

Hoy día 14 de marzo se celebra mundialmente el día de Pi, por ser su notación en algunos países, 3-14, una aproximación de dicho número.

Del número Pi sabemos muchísimas cosas: es irracional (y II) y trascendente, es protagonista de muchas fórmulas conocidas (como en áreas y volúmenes de figuras sencillas como la esfera), aparece en cuestiones relacionadas con probabilidad (como aquí), está relacionado con el conjunto de Mandelbrot, forma parte de la identidad de Euler…

…pero también hay cosas que no sabemos. Hoy vamos a comentar una de ellas, posiblemente la más importante.

No sabemos si el número Pi es un número normal en base 10

Un número normal en una base 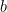$b$ es un número real que cumple que las cifras de su expresión decimal en dicha base siguen una distribución uniforme. Es decir, todos los números de una cifra aparecen en dicha expresión en la misma proporción, y lo mismo ocurre con los números de dos cifras, con los de tres, etc.

Bien, pues a estas alturas no se sabe si el número Pi es un número normal en base 10 (y de hecho, hasta donde yo sé, no se sabe si lo es en alguna otra base). Se conjetura que la respuesta a esta cuestión es afirmativa, pero no se ha podido demostrar, y tampoco se ha podido demostrar lo contrario.

Sin embargo, sí se sabe que otros números son normales en base 10, como el número de Champernowne

$0,1234567891011121314151617181920212223 \ldots$

cuyos decimales se obtienen concatenando los números enteros positivos, o el número de Copeland-Erdös

$0,23571113171923 \ldots$

cuyos decimales son la concatenación de los números primos.

¿Será el número Pi un número normal en base 10? Pues estadísticamente es lo más probable, ya que el conjunto de los números normales en base 10 es mucho mayor que el conjunto de los no normales (aun siendo ambos conjuntos infinitos), aunque evidentemente esto no demuestra nada.

Recomiendo leer el artículo No es seguro que todo el universo esté contenido en Pi, pero sí en otros números, de David Orden, en el que habla sobre este tema y proporciona muchos enlaces con información adicional.

Bonus: un par de cuestiones más que no conocemos sobre el número Pi

Y para terminar este artículo os dejo un par de cuestiones más que tampoco conocemos sobre esta maravilla de constante matemática que es el número Pi:

¿Son los números $\pi+e$ , $\pi \over e$ y $log(\pi)$ irracionales?
Tanto $\pi$ como $e$ son irracionales (sobre lo segundo tenéis una demostración aquí y otra aquí), y de hecho se sabe que son trascendentes (del segundo podéis ver una prueba aquí), pero no se sabe si $\pi+e$ y/o $\pi \over e$ son también irracionales (y mucho menos si son trascendentes). No parece fácil demostrar si es cierto o falso que lo sean, pero ahí queda por si alguien quiere intentarlo.

Lo mismo ocurre con $log(\pi)$ . Se sabe que el logaritmo decimal de un número racional es un número entero o un número irracional, pero no se sabe qué ocurre con $log(\pi)$ . Otro problema (difícil) que podéis atacar si os veis con ganas.
¿Está la constante de Apéry relacionada con el número Pi?
El problema de Basilea consiste en calcular el valor de la suma de los inversos de los cuadrados de los enteros positivos. Es decir, al cálculo del valor de la siguiente suma infinita:

$\displaystyle{\sum_{n=1}^{\infty} \cfrac{1}{n^2}}$

Leonhard Euler determinó que el valor de dicha suma es $\pi^2 \over 6$ (aquí tenéis otra demostración). Pero Euler hizo más: determinó los valores de las sumas correspondientes a los inversos de las potencias cuartas, sextas, y así hasta ¡¡26!! de los enteros positivos…y resultó que todas se relacionan de alguna forma con el número Pi. Por ejemplo:

$\cfrac{\pi ^6}{945}=\cfrac{1}{1^6}+\cfrac{1}{2^6}+\cfrac{1}{3^6}+\cfrac{1}{4^6}+\cfrac{1}{5^6}+ \dots$

Pero Euler no dijo nada sobre los inversos de las potencias impares. De hecho ni siquiera se sabe cuál es el valor para exponente 3. Es decir, no se conoce el valor de la siguiente suma:

$\displaystyle{\sum_{n=1}^{\infty} \cfrac{1}{n^3}}$

que se denomina constante de Apéry, porque fue Roger Apéry quien demostró en 1977 que el resultado de esta suma infinita es un número irracional.

Teniendo en cuenta que parece que los valores para exponente par se relacionan todos con el número Pi (aunque ahora mismo no sé si hay algún resultado que afirme esto para todo exponente par), no es descabellado pensar que para potencias impares pudiera pasar lo mismo. Ahora, no se sabe nada sobre ello, ni afirmativa ni negativamente. ¿Lo sabremos algún día? Esperemos que sí.