En matemáticas, la fórmula de Viète, es una fórmula debida a François Viète, que proporciona una representación del número π como un producto infinito
La expresión anterior tiene especial relevancia por ser el primer ejemplo conocido de una expresión exacta precisa del número π, a diferencia de las aproximaciones racionales manejadas en la antigüedad.
Deducción[editar]
Aunque la fórmula anterior proporciona la primera expresión analítica para π, se obtiene mediante la aplicación de identidades trigonométricas a un razomamiento geométrico relacionado con el problema de la cuadratura del círculo
El proceso consiste en inscribir, en un círculo de radio 1, polígonos regulares de  lados de modo que la sucesión de las áreas resulta una aproximación sucesiva al área del círculo, igual a π.
lados de modo que la sucesión de las áreas resulta una aproximación sucesiva al área del círculo, igual a π.
 lados de modo que la sucesión de las áreas resulta una aproximación sucesiva al área del círculo, igual a π.
lados de modo que la sucesión de las áreas resulta una aproximación sucesiva al área del círculo, igual a π.
Si  es el área del polígono inscrito de 2n lados entonces
es el área del polígono inscrito de 2n lados entonces
 es el área del polígono inscrito de 2n lados entonces
es el área del polígono inscrito de 2n lados entonces.
Por otro lado, la fórmula de seno de ángulo doble establece que
y por tanto
.
Combinando ambos resultados se llega a las fórmulas:
Y como los valores de  (las áreas de los polígonos) se aproximan al área del círculo que vale π, se tiene
(las áreas de los polígonos) se aproximan al área del círculo que vale π, se tiene
 (las áreas de los polígonos) se aproximan al área del círculo que vale π, se tiene
(las áreas de los polígonos) se aproximan al área del círculo que vale π, se tiene
El área de 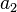 es el área de un cuadrado inscrito en un círculo de radio 1, por lo que
es el área de un cuadrado inscrito en un círculo de radio 1, por lo que  . Así, se obtiene
. Así, se obtiene
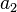 es el área de un cuadrado inscrito en un círculo de radio 1, por lo que
es el área de un cuadrado inscrito en un círculo de radio 1, por lo que  . Así, se obtiene
. Así, se obtiene
Finalmente, la fórmula del ángulo doble para el coseno implica
.
y como para  se cumple
se cumple
 se cumple
se cumple.
la sustitución repetida en la expresión para  concluye la prueba.
concluye la prueba.
 concluye la prueba.
concluye la prueba.
Sin embargo, aunque la prueba anterior es geométricamente intuitiva, una demostración rigurosa involucra demostrar la convergencia de los productos infinitos, herramienta matemática que no se disponía durante la época de Viète por lo que no fue sino más de un siglo después cuando Euler proporcionó una prueba formal.











No hay comentarios:
Publicar un comentario