nymanmatematico: 14 de Marzo El día de Pi de Gaussianos

Hoy es 14 de marzo y, como todos los años, en esta fecha se celebra mundialmente el día de Pi por ser 3-14 la notación que se utiliza para este día en ciertas zonas de nuestro planeta. Además, añadiendo las dos últimas cifras de este año 2016, en esta ocasión tenemos la típica aproximación a cuatro decimales que todos aprendimos en su momento de este interesantísimo número irracional: 3.1416.

Mucho hemos hablado en Gaussianos sobre Pi (en la categoría Pipodéis ver la gran cantidad de artículos en los que aparece), y todos los años hemos celebrado este bonito día 14 de marzo (al final de esta entrada tenéis los enlaces a los artículos publicados en este blog el día de Pi). Y, para no poder las buenas costumbres, este año vamos a volver a hacerlo.

En esta ocasión vamos a celebrar el día de Pi destacando elprimer producto infinito conocido con Pi como protagonista. Se trata de la conocida como fórmula de Viète, publicada porFrançois Viète en 1593 como parte de su obra Variorum de rebus mathematicis responsorum, liber VIII. Dicha fórmula es la siguiente:

$\cfrac2\pi= \sqrt{\cfrac12} \cdot\sqrt{\cfrac12 +\cfrac12\sqrt{\cfrac12}}\cdot\sqrt{\cfrac12 +\cfrac12 \sqrt{\cfrac12 + \cfrac12\sqrt{\cfrac12}}}\cdot\sqrt{\cfrac12+\cfrac12\sqrt{\cfrac12 +\cfrac12 \sqrt{\cfrac12 + \cfrac12\sqrt{\cfrac12}}}}\cdots$

Al parecer, no solamente se trata del primer producto infinito en el que aparece el número Pi, sino del primer desarrollo infinito que involucra a dicho número. Viendo que hasta ese momento sólo se disponía de aproximaciones para Pi, el descubrimiento de esta expresión puede considerarse como un hito histórico, así como un gran avance de las matemáticas en su conjunto.

La idea que usó Viète fue partir de un círculo de radio 1 (cuya área es exactamente 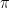$\pi$ ) e inscribir en él polígonos de 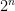$2^n$ lados, para $n \geq 2$ , comparando después las áreas de los polígonos de $2^k$ y $2^{k+1}$ lados. Pero hay una manera relativamente sencilla de deducir la fórmula de Viète utilizando identidades trigonométricas:

Si inscribimos un polígono regular de $2^n$ lados en un círculo de radio 1, es sencillo ver, triangulando dicho polígono, que el área del mismo, $a_n$ , se puede expresar así:

$a_n=2^n \; sen \left ( \cfrac{\pi}{2^n} \right ) \; cos \left ( \cfrac{\pi}{2^n} \right )$

Usando la fórmula de seno de ángulo doble, $sen(2 \alpha)=2sen(\alpha)cos(\alpha)$ , llegamos a que:

$a_2=a_3 \; cos \left ( \cfrac{\pi}{2^2} \right )=a_4 \; cos \left ( \cfrac{\pi}{2^2} \right ) cos \left ( \cfrac{\pi}{2^3} \right )=a_5 \; cos \left ( \cfrac{\pi}{2^2} \right ) cos \left ( \cfrac{\pi}{2^3} \right ) cos \left ( \cfrac{\pi}{2^4} \right )=\ldots$

Como $a_n$ tiende a $\pi$ cuando $n \to \infty$ (el área del círculo), se tiene que:

$a_2=\pi \; cos \left ( \cfrac{\pi}{2^2} \right ) cos \left ( \cfrac{\pi}{2^3} \right ) cos \left ( \cfrac{\pi}{2^4} \right ) cos \left ( \cfrac{\pi}{2^5} \right ) \ldots$

Ahora, $a_2$ es el área del cuadrado inscrito en el círculo anterior, cuyo valor es 2, por lo que de la expresión anterior obtenemos lo siguiente:

$\cfrac{2}{\pi}=cos \left ( \cfrac{\pi}{2^2} \right ) \; cos \left ( \cfrac{\pi}{2^3} \right ) \; cos \left ( \cfrac{\pi}{2^4} \right ) \; cos \left ( \cfrac{\pi}{2^5} \right ) \ldots$

Usando ahora la fórmula para el seno del ángulo mitad, $cos \left ( \frac{\alpha}{2} \right )=\sqrt{\frac{1+cos(\alpha)}{2}}=\sqrt{\frac{1}{2}+\frac{1}{2} cos (\alpha)}$ , y que $cos(\frac{\pi}{2^2})=\sqrt{\frac{1}{2}}$ llegamos a la expresión de la fórmula de Viète.

Un último apunte interesante sobre esta fórmula de Viète. En 1655, John Wallis encontraba el siguiente desarrollo infinito para $2 \over \pi$ :

$\cfrac{2}{\pi}=\cfrac{1 \cdot 3}{2 \cdot 2} \cdot \cfrac{3 \cdot 5}{4 \cdot 4} \cdot \cfrac{5 \cdot 7}{6 \cdot 6} \cdot \cfrac{7 \cdot 9}{8 \cdot 8} \ldots$

En principio, ambas fórmulas no parecen tener mucha relación, pero hace pocos años se demostró que no es así. En 1999, Thomas J. Osler publicaba en American Mathematical Monthly una fórmula que incluye como casos particulares tanto a la fórmula de Viète como a la fórmula de Wallis. Podéis ver el artículo en The union of Vieta’s and Wallis’ products for Pi (pdf). También podéis ver comentarios sobre la misma en Historia de las fórmulas y algoritmos para 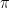$\pi$ (pdf), de Jesús Guillera, artículo en el que también encontraréis muchas más información sobre el tema.

Entrada destacada

lunes, 14 de marzo de 2016

14 de Marzo El día de Pi de Gaussianos

No hay comentarios:

Buscar este blog