Una de las pasiones del famoso matemático John Nash fue la Teoría de Juegos en la que aportó significantes resultados. Pero lo que le proponemos hoy es algo más sencillo y asequible para todos que estos estudios de Nash: se trata de un juego para dos jugadores para el que sólo se necesita lápiz y papel. O, si tienen, losetas hexagonales en el suelo de casa, como hacía el propio Nash con sus estudiantes en Princeton.
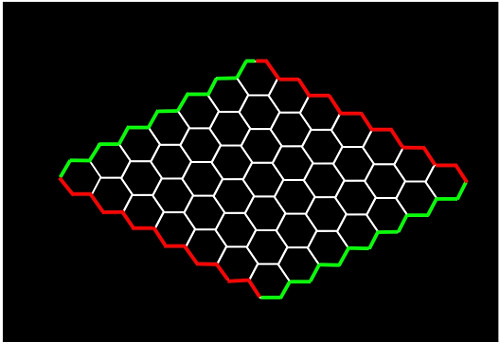
El juego se llama Hex porque las casillas del tablero son precisamente hexágonos: sólo hay que dibujar un rombo usando hexágonos, como por ejemplo este:
Este es un tablero 7 por 7, aunque lo usual es jugar en un tablero, al menos, 10 por 10. Hemos pintado dos lados de rojo y otros dos de verde. Ahora, cada jugador tendrá 25 fichas: uno de ellos fichas verdes y el otro fichas rojas, o un rotulador verde y otro rojo en su defecto. Y saber que solo podrán colorear 25 casillas, claro.
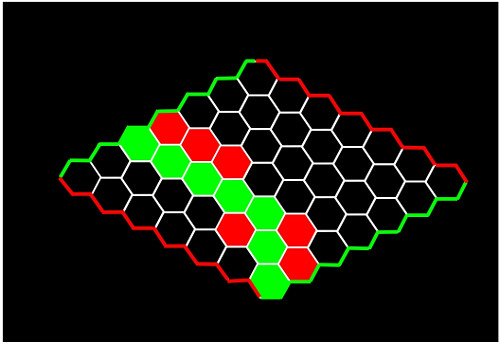
Por turnos, los jugadores, van poniendo sus fichas en el tablero sin ninguna restricción, y gana el que consiga un camino que una los dos lados de su color correspondiente. Por ejemplo, en la partida que aparece en la siguiente figura, habrían ganado las fichas verdes.
Ea, ya pueden empezar a jugar. Pero antes déjenme que les cuente algunas curiosidades del juego.
Lo primero es que es imposible quedar en tablas: uno de los dos jugadores gana seguro. Esto se puede demostrar usando razonamientos de Teoría de Grafos pero, básicamente, la idea de la demostración es que si llenas el tablero de fichas rojas y verdes, de todas las formas posibles, siempre tiene que haber o un camino rojo conectando los lados rojos, o un camino verde conectando los lados verdes. Fue David Gale el que lo demostró en 1979, y que este hecho implicaba el teorema del punto fijo de Brouwer, pero esto último es un poco complicado de explicar aquí.
Por otra parte, nuestro protagonista demostró que en cualquier tablero, de cualquier dimensión, existe una estrategia ganadora para el primer jugador. Eso sí, fue una demostración teórica. En la práctica, hasta donde yo sé, solo se han descrito dichas estrategias para tableros de hasta 9 x 9.
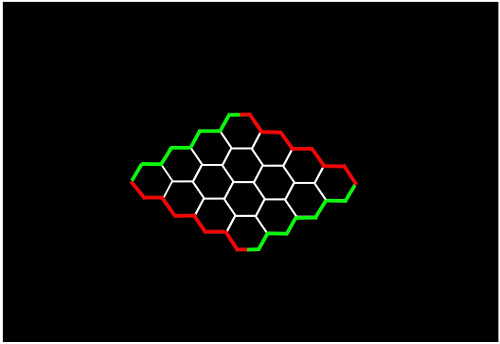
Les cuento, por simplicidad, la estrategia ganadora en un 4 x 4, que igual les viene bien este verano para jugar en la piscina, en la playa o en el salón de casa.
Dibujamos el tablero de estas dimensiones:
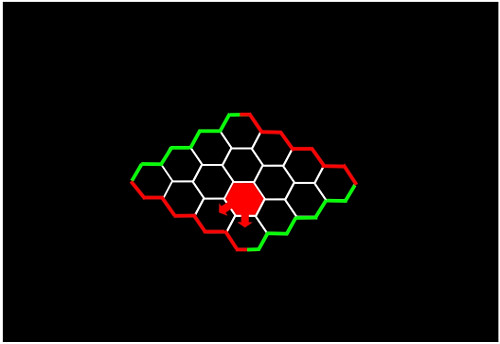
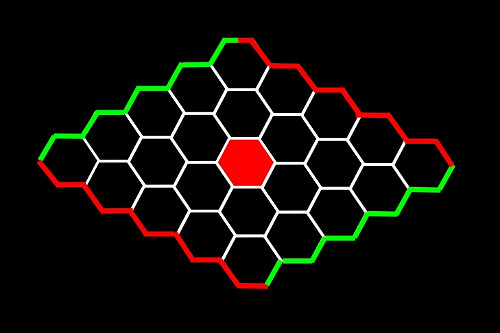
Pues bien, si el primer jugador coloca su primera ficha en la posición indicada en la siguiente figura, ya ha ganado.
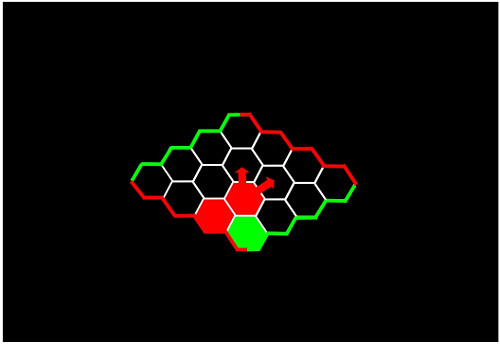
Basta que coloque la segunda ficha roja en una de las dos posiciones indicadas por las flechas. Haga lo que haga el jugador de verde, una de ellas quedará libre. Con eso, el jugador rojo ya alcanzó uno de los lados rojos del rombo.
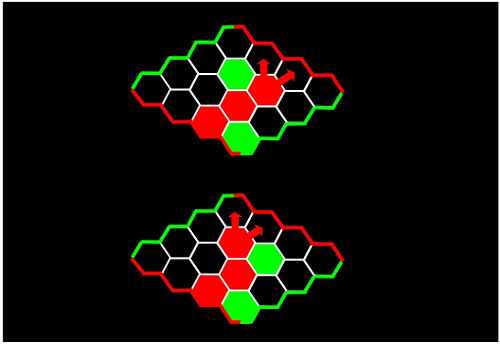
Sea lo que sea lo que haya ocurrido en la segunda jugada del rojo, la tercera ficha que ponga debe estar en una de las dos posiciones señaladas con flechas en la siguiente ilustración. Otra vez, una de ellas quedará libre tras jugar el verde.
Por último, en función de lo que haya hecho este segundo jugador, el verde, tenemos todos los posibles movimientos que dan la victoria al rojo señalados con flechas:
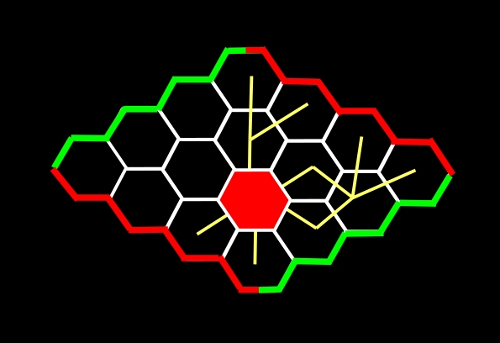
Básicamente, si el primer jugador (el rojo) comienza en esa posición, puede siempre elegir un camino para llegar a los dos bordes rojos, siguiendo algunas de las rutas marcadas en la siguiente ilustración en amarillo.
Como ven, la estrategia ganadora de este tablero es muy simple, pero seguro que les sirve para ganarse algún café a la hora del desayuno.
Ah, la estrategia ganadora para el primer jugador en el tablero 5 x 5 comienza así:
Les dejo que adivinen el resto. Si se rinden, estaré pendiente de los comentarios.
Según parece, la invención de este juego llamado Hex se atribuye tanto a Nash como al matemático danés Piet Hein, porque lo descubrieron a la vez de forma independiente. Eso sí, en la Universidad de Princeton le llamaban 'el juego Nash' e incluso 'el juego John' en su honor.
Cuando dio con él Nash buscaba el juego perfecto para los matemáticos, y cuentan que él creía que era el Hex de 14 x 14.
Sacado de



No hay comentarios:
Publicar un comentario