Carl Friedrich Gauss: el príncipe de las matemáticas

Johann Carl Friedrich Gauss nació el 30 de abril de 1777 en Brunswick, Alemania, y murió el 23 de febrero de 1855 en Göttingen, también en el país teutón. Sus estudios e investigaciones pueden localizarse tanto en matemáticas como en física y astronomía. Posiblemente la teoría de números sea la rama de las matemáticas en la que la influencia ejercida por Gauss haya sido mayor (recordemos sus propias palabras sobre ella). Pero ni muchos menos la cosa se queda ahí. Las aportaciones de Gauss a la geometría diferencial, al análisis matemático, a la estadística o al a geodesia son realmente notables.

Podemos decir que Gauss fue un niño prodigio en lo que se refiere a las matemáticas en general y al cálculo en particular. A los 3 años de edad corrigió a su padre una operación que estaba realizando relacionada con pagos de salarios a los trabajadores que tenía a su cargo. Pero puede que la anécdota más conocida de su infancia sea la ocurrida cuando contaba con 7 años de edad (y que ya comentamos en el primer post de la historia de Gaussianos). Estando en el colegio, en uno de esos típicos momentos de barullo entre niños de esa edad su profesor J.G Bütner castigó a toda la clase con sumar todos los números naturales desde el 1 hasta el 100. Casi de forma instantánea Gauss tenía la respuesta correcta: 5050 (los detalles los podéis encontrar en el post enlazado hace unas líneas). La cuestión es que este hecho, junto con muchos otros, contribuyeron a que los profesores de Gauss vieran en él algo especial, una especie de don para las matemáticas, y que hablaran con sus padres para permitirle recibir clases complementarias de matemáticas después de las clases ordinarias.

Quizás esas son las dos anécdotas más conocidas de la infancia de nuestro personaje, pero no son las únicas. Poco después de cumplir 10 años Gauss ya había descubierto dos métodos para calcular raíces cuadradas de números de 50 cifras decimales y cuentan que en esa época encontró pequeños errores en tablas logarítmicas que cayeron en sus manos. Sencillamente impresionante.

En 1788 ingresó en el Gymnasium local (escuela secundaria) y aprendió principalmente cultura clásica. Su formación matemática continuó a través de instrucciones particulares y mediante la lectura de libros, entre los que se encuentran obras de arte como los Principia de Newton o el Ars Conjectandi de Bernoulli. Tal fue la fama que adquirió en el Gymnasium que a los 15 años el duque de su ciudad natal apoyó a Gauss económicamente para que siguiera estudiando en el Collegium Carolinum de Brunswick.

Al comienzo de esta etapa de sus estudios se puede decir que Gauss ya poseía suficientes conocimientos como para haberse graduado. En 1795 dejó el centro habiendo hecho tantas matemáticas como para terminar una carrera. En esta época comenzaron sus propuestas de aproximación de la función $\pi(n)$ (función que cuenta los números primos menores o iguales a $n$ ). Comenzó proponiendo:

$\pi(n) \approx \cfrac{n}{Ln(n)}$

para después ajustar más con:

$\pi(n)=\displaystyle{\int_2^n \cfrac{dx}{Ln(x)}}$

Su gran capacidad para el cálculo le permitió comprobar dicha fórmula hasta $n=3000000$ .

Después del Collegium eligió la Universidad de Göttingen para sus estudios, posiblemente debido a que ésta poseía una gran biblioteca matemática. Revisando los registros de dicha biblioteca sorprende el hecho de que Gauss retirara más libros de Humanidades que de Matemáticas. Pero este hecho no supuso, ni muchísimo menos, que se retirara de esta ciencia. Más bien todo lo contrario.

Su primer gran resultado fue la demostración de que se puede construir un heptadecágono (polígono regular de 17 lados) con regla y compás en el sentido clásico de este tipo de construcciones. A partir de este hecho demostró un resultado más general sobre construcciones con regla y compás que recuerdo aquí aunque en Gaussianos ya lo conocemos:

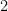
Un polígono regular de $n$ lados es construible con regla y compás (en el sentido clásico de estas construcciones) si $n$ es igual al producto de una potencia de $2$ por un cierto número de primos de Fermat distintos, es decir:

$n=2^s \cdot p_1 \cdot \ldots \cdot p_k$ , siendo $p_k$ primos de Fermat distintos.

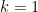
Por tanto, para $s=0$ y $k=1$ se tiene que todo polígono regular cuyo número de lados es un primo de Fermat es construible con regla y compás. Como $17$ es uno de ellos, el heptadecágono es construible de esta forma.

Gauss estaba tan orgulloso de la demostración de este resultado que decidió estudiar Matemáticas por él.

Estando todavía en la universidad Gauss realizó otros importantes descubrimientos, entre los que destacan los siguientes:

Inventó la aritmética modular (y II), hecho que sirvió para unificar la teoría de números.
Demostró la ley de reciprocidad cuadrática, enunciada pero no demostrada completamente por Legendre unos años antes.
Demostró que todo número número entero positivo puede expresarse como suma de como mucho tres números triangulares (en su diario podía leerse ¡Eureka! num= $\triangle + \triangle + \triangle$ ).

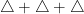Dos años en Göttingen le bastaron para darse cuenta de que ya nadie podía hacerle avanzar allí. Por ello volvió a su casa en Brunswick a escribir su tesis doctoral. Como tema central de la misma eligió el teorema fundamental del álgebra, que dice que todo polinomio de grado $n$ con coeficientes complejos tiene exactamente $n$ raíces complejas(aunque bastaría formularlo así: todo polinomio de grado $n$ con coeficientes complejos tiene al menos una raíz compleja). Aunque en la actualidad su primera demostración no está aceptada, las otras tres demostraciones del mismo resultado que produjo durante su vida sí son plenamente correctas.

En 1801 Gauss publico en su obra Disquisitiones Arithmeticae. En ella, a partir de la aritmética modular (congruencias), reunió una gran cantidad de resultados relacionados con teoría de números (la ley de reciprocidad cuadrática entre ellos). Esta publicación contribuyó de manera fundamental a la sistematización de dicha rama de las matemáticas. En este enlace podéis encontrar una versión digital de la primera traducción al español de dicha obra.

Después de esto Gauss añadió la astronomía a su radio de acción. Este mismo año 1801 el astrónomo italiano Giuseppe Piazzi observó lo que pensó que era un planeta, pero le perdió la pista demasiado pronto. Gauss predijo que no era un planeta, sino un asteroide, utilizando elipses en vez de circunferencias para modelizar las órbitas y creando el método de mínimos cuadrados para minimizar los errores de medida cometidos. A finales de 1801 los astrónomos encontraron el asteroide Ceres exactamente donde Gauss predijo que estaría.

Otro de los campos a los que Gauss le dedicó parte de su tiempo fue la geodesia, es decir, las matemáticas que describen y representan la Tierra. En 1817, después de dos décadas sin interesarse por esta rama, fue nombrado responsable de un estudio geodésico en Hannover. Después de inspeccionar tierra y tomar datos durante gran parte de tiempo Gauss no estaba demasiado satisfecho con las técnicas geodésicas del momento. Por ello inventó el heliotropo, instrumento que utiliza espejos para dirigir los rayos de luz a través de aperturas pequeñas de telescopios.

Pero quizás la incursión de Gauss en las geometrías no euclídeas sea la espina clavada en la vida matemática de nuestro protagonista. A la vista de sus cuadernos parece ser que Gauss fue la primera persona que intuyó que eliminando el quinto postulado de la geometría euclídea se podía crear una geometría tan consistente como ella, pero por falta de datos empíricos decidió no publicar ninguno de sus trabajos ni comunicárselos a nadie…hasta que János Bolyai descubrió ese mismo resultado de forma independiente. Cuando Gauss tuvo conocimiento de dicho trabajo envió una carta al padre de Bolyai en la que se puede leer el siguiente párrafo:

Alabarlo sería como alabarme a mí mismo. Todo el contenido del trabajo…coincide casi exactamente con mis propias meditaciones, las cuales ha ocupado mi mente durante los pasados treinta y cinco años.

La familia Bolyai no se tomó demasiado bien estas palabras al creer que Gauss quería atribuirse este descubrimiento.

En este mismo campo podemos destacar que fue el encargado de la ponencia que tuvo que exponer Riemann para confirmar su habilitación en Göttingen, relacionada con la geometría no euclídea (además de supervisar la tesis doctoral del mismo Riemann que versaba sobre lo que ahora se conoce como superficies de Riemann).

Por otra parte, en la época de sus estudios de Hannover también se interesó por la geometría diferencial. Sobre este campo publicó Disquisitiones generales circa superficies curva, donde demostró su gran resultado en esta rama: el teorema egregium. De esta obra derivó también el concepto de curvatura de Gauss.

Otro de los campos en los que se introdujo Gauss fue la estadística. En 1823 publicó Theoria combinationis observationum erroribus minimis obnoxiae, dedicada a la distribución normal. La representación gráfica de la función de densidad de dicha distribución es la denominada campana de Gauss (podéis verla en la imagen de la izquierda para distintos valores de su media $\mu$ y su desviación típica $\sigma$ ). 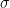Tanto esta curva como su distribución de probabilidad son en la actualidad enormemente útiles para muchísimos estudios relacionados con distribuciones de datos y su facilidad para ajustarse como modelo a situaciones muy diversas la convierte en una herramienta fundamental en muchos campos de estudio..

Algunos otros descubrimientos y resultados que han terminado llevando el nombre de Gauss son los siguientes:

El teorema de Gauss-Bonnet
El método de Gauss para triangular una matriz (y el método de eliminación de Gauss-Jordan).
El método de Gauss-Seidel (método iterativo para resolver sistemas de ecuaciones lineales).
El teorema de la divergencia, conocido también como teorema de Gauss (y por teorema de Ostrogradsky-Gauss).

Podéis encontrar una lista más completa aquí (en inglés).

Para terminar, comentar que Gauss no se mostraba demasiado ilusionado con el hecho de tener que impartir clases. De hecho posiblemente el no tener la obligación de impartirlas durante gran parte de su vida debió ser una de las razones por las que Gauss pudo avanzar tantos en todos los campos de la ciencia en los que se involucró. A pesar de eso entre sus alumnos se encuentran grandes personalidades de la historia de las matemáticas como Bessel, Dedekind o el ya nombrado Riemann.

Charles John Huffam Dickens fue un escritor y novelista inglés, uno de los más reconocidos de la literatura universal, y el más sobresaliente de la era victoriana. Fue maestro del género narrativo, al que imprimió ciertas dosis de humor e ironía, practicando a la vez una aguda crítica social.

Fecha de nacimiento: 7 de febrero de 1812, Landport, Portsmouth, Reino Unido

Fallecimiento: 9 de junio de 1870, Gads Hill Place, Reino Unido

Novelas

Los papeles póstumos del Club Pickwick (1836-1837)
Oliver Twist (1837-1839)
Nicholas Nickleby (1838-1839)
La tienda de antigüedades (1840-1841)
Barnaby Rudge (1841)
Martin Chuzzlewit (1843-1844)
Dombey e hijo (1846-1848)
David Copperfield (1849-1850)
Casa desolada (1852-1853)
Tiempos difíciles (1854)
La pequeña Dorrit (1855-1857)
Historia de dos ciudades (1859)
Grandes esperanzas (1860-1861)
Nuestro común amigo (1864-1865)
El misterio de Edwin Drood (1870) (inacabada, publicadas seis de las doce entregas previstas)

Cuentos

Una canción de Navidad (1843) (Conocida también como Un cuento de Navidad y Los fantasmas de Scrooge)
Las campanas (1844)
El grillo del hogar (1845)
La batalla de la vida (1846)
El hechizado (1848)
Una casa en alquiler (1858)
El guardavía (1866)

Entrada destacada

jueves, 28 de febrero de 2019

Schubert ( Ave María con Mario Lanza y Pavarotti pequeñito )

Mario Lanza - Ave Maria

miércoles, 27 de febrero de 2019

Arturo Marquez ( Danzon nº 2 por Gustavo Dudamel y la Orquesta Sinfónica Simón Bolivar )

Gustavo Dudamel ~ Danzón No. 2 (Marquez) ~ Orquesta Sinfónica Simón Bolívar

viernes, 22 de febrero de 2019

Beethoven ( Misa solemne con Leonard Bernstein )

Leonard Bernstein & Concertgebouworkest Amsterdam - Beethoven: Missa solemnis

miércoles, 20 de febrero de 2019

Scriabin ( Le Poème de l'extase / Petrenko · Berliner Philharmoniker )

Scriabin: Le Poème de l'extase / Petrenko · Berliner Philharmoniker

domingo, 17 de febrero de 2019

Mozart. Ejemplo de Forma sonata : Sonata nº 16

Mozart - The Piano Sonata No 16 in C major

Lully: Le Roi Danse

Lully: Le Roi Danse

Genialidades de Mozart ( 3º movimiento sinfonia nº 39 de mozart )

Mozart - Symphony No. 39 in E flat Major(K. 543) III. Minuet: Trio

sábado, 16 de febrero de 2019